Stability -I : Chapter 1

1. A rectangular tank measures 16mx15mx6m. How many tonnes of oil of RD 0.78 can it hold?

SOLUTION:

Given : L =16m , B = 15m, H = 6m, RD=0.78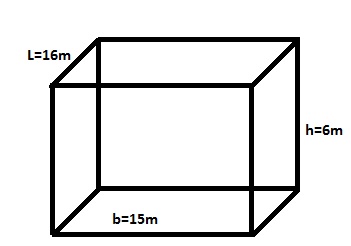

Volume of rectangle =(LxBxH)
=16x15x6
=1440m3

We know that :
Density = Mass /Volume
0.78 =Mass/1440m³

Hence, Mass =1123.2 tonnes

 

2. A cylindrical tank of diameter 8m is 10m high.400t of oil of RD 0.9 is poured in to it. Find the ullage, assuming π to be 3.1416.

SOLUTION:

Given: Diameter = 8m,

Radius = (d/2)m
=(8/2)m
=4m
Height =10m
Mass = 400t
RD =0.9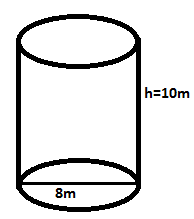

We know that:
Volume of the cylindrical tank = π²h
= 3.1416 x 4 x 4 x 10
=502.656m³

We know that:
Density = (Mass/Volume)
0.9 = 400/ (Volume of the oil)

Hence, Volume of the oil = 400/0.9
=444.44m³

Depth of oil = volume/area
Area of cylinder   =( π²r)
 =(3.1416 x 4 x 4)
 =502656m³

We can calculate Depth of oil = (volume of oil)/ ( area of cylinder)
 = (444. 44)/(50.2656 )
=8.8418 m

Hence, ullage  = (10 – 8.8418)  =1.1582m

3. A tank of 2400m³ volume and 12 depth, has vertical side and horizontal bottom. Find how many tonnes of oil of RD 0.7 it can hold, allowing 2% of the tank for the expansion .state the ullage of loading.

Solution :-

Given :
Volume of the tank = 2400m³
Depth of tank =12m
RD =0.7

According to question 2% of the volume is allowed for expansion.
As we know that

Density = Mass/ Volume
Since volume =(L x B x H)
= 2400m³( given )

So, Area = (volume / depth)
= (2400/12)
=200m²

Mass  =  ( volume x density)
Mass  =  (2400×0.7)
 =1680 t

Since 2% of the volume of the tank allowed for expansion
 = (2/100) x 2400
 = 48m³

Volume of the oil = (volume of the tank – free space )
= ( 2400 -48)
= 2352 m³

Mass of the oil = (volume x density)
 =2352 x 0.7

Depth of oil = (volume of oil /area)
= 2352/(L x B)
= (2352/ 200)
=11.76 m

Hence, Ullage = (12-11.76)
                           = 0.24m.

4. A tank 10m deep has vertical sides .its bottom consist of triangle 12mx12mx10m. find the mass of oil (of RD0.800) to be loaded , allowing 3 % of the volume of oil loaded for expansion. State the ullage on completion of loading.

Solution:

Depth of the tank = 10m
L, B, H, of triangle = (12 x 12 x 12
RD = 0.8

Allowing, 3% of the volume of the oil loaded for expansion.
Area of the triangle = 1/2 (base x height)

In triangle PQR, RQ in the height which divide the base at same length.
So In triangle PSR

SR² =PR² –PS²
= (12²– 5²)
= (144 -25)
=119

So, SR = 10.9m
So area of the triangle = 1/2 (10×10.9)
=54.5m²

Volume of the tank = (10 x54.5)
= 545m³

Now, volume of the oil = (Total volume -free space)

let ‘V’ be the volume of the oil
545 = (V + 3/100 x V)
545 = (V + 3V/ 100)
545 = (103V /100)
V = (545 x 100) /103
V = 529.126m³

Mass of the oil = (density x volume)
= 0.8 x 529.126
=423.3 t

Depth of the oil = (volume of oil)/(area)
= (529.126 /54.5)
= 9.7087m

Ullage = ( 10 – 9.708)
                 = 0.292m

5. A rectangular tank measuring 25mx 12m x8m has an ullage pipe projecting 0.3m above the tank top. find the mass of SW in the tank when the ullage is 3.3m.

Solution :

Volume of the rectangular tank = ( L x B x H)
= (25 x 12 x 8 )

Pipe above the tank top is 0.3m

Total ullage =3.3m

Ullage inside the tank = (3.3 – 0.3)
= 3m

Depth of the SW = (8 – 3)
= 5m

Volume of the SW = (L x B x H )
= ( 25 x12 x5)
= 1500 m³

Mass of the SW = (volume x density)
                                 = (1500 x1.025)
                                 = 1537.5 t

6. A rectangular tank measures 30mx 16mx 14m. It has an ullage pipe projecting 0.5m above its top. Oil of RD 0.78 is to be loaded . The pipe line leading from the refinery to the ship is 10km long and 40cm in diameter. At the time of completion, all the oil in pipeline has to be taken. find at what ullage the valve at the refinery end must be shut so that the final ullage in the ship’s tank would be 0.78m. State also, the mass of oil loaded finally. (Assume π to be 3.1416).

Given :

The volume of the rectangular tank = (L x B x H)
=(30 x16 x14)
Ullage pipe projecting above its top = 0.5m
RD of oil = 0.78
The length of the pipe line from tank to the ship = 10km
= 10000m
The diameter of the pipe = (d)
= 40cm
Hence, radius = (40 /2 )
= 20cm

Volume of the tank = (L x B x H)
= (30m x16m x14m)
 =6720m³

Area = (L x B)
 = (30 x 16)
 = 480m²

The total ullage =0.78m

So ,ullage inside the tank = (0.78 –  0.50)
= 0.28m

If ullage inside the tank = 0.25m,The depth of oil to be loaded is
 = (14 -0.28) m
 =13.72m

Volume of the oil = (L x B x D)
=( 30x 16x 13.72)m
= 6585.6 m³

Mass of the oil to be load = (volume x density)
= (6585.6 x 0.78)
= 5136.768 t

Now , volume of oil in the pipe  = (πr²h)
 =(3.1416 x 0.2 x 0.2 x 10000)
=1256.64m³

Depth of oil when it poured in to the tank = (volume /area)
= (1256.64 /480)
= 2.618m

Depth of the tank without the pipe line oil = (13.72 -2.618)
 = 11.102m

Thus the ullage will be = (14 -11.102)
= 2.898m

Exact ullage where pump should be shut = (2.898 + 0.5)m
                                                                             = 3.398m.

7. A tank with a horizontal base and vertical sides is 10m deep and has rectangular trunkway 1m high. The volume of the tank alone is 8000m3 and that of the trunkway 500m³ . Find the ullage when 5320t of vegetable oil of RD 0.7 is loaded.

Given :

The depth of tank = 10m
Height of the trunkway = 1m
Volume of the tank alone =8000m³
Volume of the trunkway = 500m³
The mass of the oil =5320 t
RD =0.7

We know that :
Density = (mass /volume)
Volume   = mass /density
 = (5320 /0.7)
 = 7600m³

Depth of oil = (volume /area)
= (7600/800)
=9.5m

Ullage insides the tank = (10 – 9.5)
=0.5m

Total ullage = (1 +0 .5)
                          = 1.5m.

8. A rectangular tank has a total depth of 21m and volume of 20600 m³, which includes of trunkway of depth 1m and volume 600m³. find the ullage when 16320 t of oil of RD 0.8 is loaded.

Given :

The total depth of tank =21m
Volume of the tank = 20600m³
The height of the trunkway = 1m
Volume of the trunkway =  600m³
Oil loaded = 16320t
RD= 0.8
The height of the tank = (21-1)
= 20m

Volume of the tank= (20600 – 600)
 =20000m³

Area of tank = (20000 /20)
=10000m²

Volume of the oil = (mass /density)
=(1620 /0.8)
= 20400 m³

Hence, Volume of the oil inside the trunkway = (Total volume of the oil – volume of the tank)
= (20400 – 20000)
 =400m³

Depth of the oil = (volume /area)
= (400/600)
 = 0.66m

Hence, Ullage = (1 -0.66)
                             = 0.33m

9. A rectangular tank has a total depth of 10.5m and volume 8200m3, which include a trunkway of depth 0.5 m and volume 200m³ . find the mass of oil of oil of RD 0.8 loaded and the ullage, if 2% of the volume of the tank is left for expansion.

Given :

Depth of the tank is = 10.5m
Volume of the tank = 8200m³
Depth of the trunkway = 0.5m
Volume of the trunkway = 200m³
RD of the oil = 0.8

According to question, 2% of the tank volume left for expansion .
Volume of the tank alone = (8200-200)
= 8000m³

Height of the tank alone = (10.5 -0.5)
= 10 m

2% of the volume of the tank left for expansion .
= (2/100 x 8200)
=164m³

Volume of the oil to be load = (8200 -164)
=8036 m³

Mass of oil to be load = ( volume x density)
= (8036 x 0.8)
= 6428.8t

Volume of the trunkway = (L x B x 0.5)
= 200m³ ( given)

We can calculate Area as = (200 /0.5)
=400m²

Volume of the free space = ullage= (volume of the free space)/(area)
                                                                   = (164/ 400)m
                                                                   =0.41m.

10. A rectangular tank has a total depth of 21m and volume 10250m³ which include a trunkway of trunkway of depth 1m and volume 250m3. Oil of RD 0.9 is to be loaded for expansion. find the mass of oil to be loaded and the final ullage.

Given :

Total depth of the tank =21m

Total volume of the tank =10250m³
RD =0.9

According to question , Space left for expansion is
=(3% of the volume of the oil)

Let ‘v’ be the volume of the oil
3 /100 x v = volume of free space
(Volume of free space) + (volume of oil) = (volume of tank)
( 3/100 x v + v ) = 10250m³
(3v /100 + v) = 10250m³
(103v /100)  = 10250m³
V = (10250×100 /103)
 = 9951.456m³

Volume of the free space = (10000 -9951.456) m³
= 48.544m³

Depth of the free space = (volume / area )
= (48.544 /500)
= 0.0970m

Hence ,  final  Ullage  =( 1.0 + 0.0970)
                   = 1.097m .