C L DUBEY – EXERCISE – 02 : Simpson’s Rule

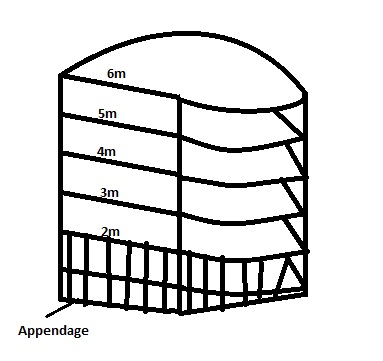
Q1. The TPC of a ship are as follows:

Draft (m)	6.0	5.0	4.0	3.0	2.0
TPC	22.45	22.04	21.53	20.91	19.68

The displacement and KB at 2m draft are 3280t and 1.2m respectively. Find the displacement and KB at 6m draft in SW.

Solution –

Given,

Draft	TPC	Area (TPC= A/100 ⨯ density)	SM	Product	Lever	Moment
6.0	22.45	(100)⨯22.45/1.025	1	22.45x	4h	89.8xh
5.0	22.04	22.04x	4	88.16x	3h	264.48xh
4.0	21.53	21.53x	2	43.06x	2h	86.12xh
3.0	20.91	20.91x	4	83.64x	1h	83.64xh
2.0	19.68	19.68x	1	19.68x	0h	0

Sum of product of volume = 256.99x
Volume = 1/3 ⨯ 256.99 ⨯ 100/1.025
= 8357.398m³

Sum of product of moment = 524.04 ⨯ 1/3 ⨯ 100/1.025 ⨯ 1
= 17041.95m⁴

Total volume including appendage =?
Given displacement of appendage = 3280 tonnes at draft 2m
We know displacement = ( v/w volume X  density of water displaced)
Volume of appendage = 3280/1.025
= 3200m³

Total volume including appendage = (8357.398 + 3200) m³
= 11557.398 m³

COG of the structure without appendage
= volume/Moment
= 2.039m

COG from 2.0 mtr draft = 2.039 m
Now total moment = moment of appendage + moment of structure
11846.33 ⨯  X   = (3280 ⨯ 2) + (8566.33 ⨯ 4.039)

 X = 3.253m

Q2. The breadths of a ship’s water-plane 120m long, measured at equal intervals from aft, are: 1.2, 9.6, 13.2, 15.0, 15.3, 15.6, 15.6, 14.7, 12.9, 9.0 and 0.0m respectively. Find:

• The water plane area;

• TPC in sea water;

• FWA if displacement is 6690t.

Solution –

Ordinate		SM	Product
1.2		1	1.2
9.6		4	38.4
13.2		2	26.4
15.0		4	60.0
15.3		2	30.6
15.6		4	62.4
15.6	2		31.2
14.7	4		58.8
12.9	2		25.8
9.0	4		36.0
0.0	1		0.0
			370.8