A wall-sided inclination of the ship is one where the waterline on both sides of the ship is in contact with the vertical sides of the ship i.e. the ship is not inclined beyond the angle of heel at which the deck edge becomes immersed or an angle of heel where the turn of the bilge becomes exposed above the waterline.
The distinction between stability at small and large angles of heel by consideration of the Wall-sided Formula
Stability at small angles of heel (initial stability)
A ship heeled to a small angle by an external force. The centre of buoyancy has moved from B to B1, which is a movement parallel to, and in the same direction as, the shift of the wedge of buoyancy from b to b1.
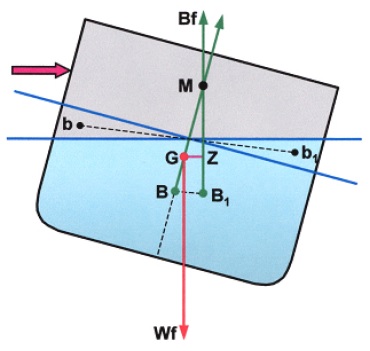
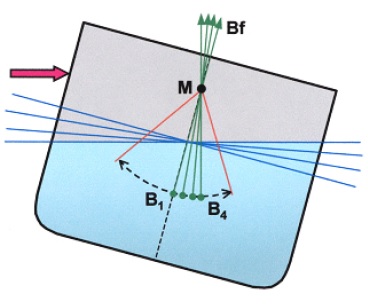
The line of action of buoyancy force acting upwards through B1 passes through the initial transverse metacentre (M). For small angles of heel (up to about 6º) it is assumed that the movement of B to the low side follows the arc of a circle, BM being the radius of the arc known as the metacentric radius.
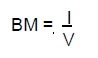
where I is the second moment of area (or moment of inertia) of the water plane area. For a box-shaped vessel:
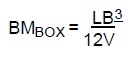
where L and B are the length and breadth of the water plane area respectively and V is the volume of displacement of the vessel (L x B x d).
For small angles of heel the BM can be assumed constant, since there is no significant increase or change of shape of the water plane area as the ship heels, since the value of I must also be assumed constant.
Under these conditions righting lever may be calculated using:
![]()
and the moment of statical stability or righting moment is given by:
![]()
This measure of stability is referred to as initial stability because it is related to the position of the initial transverse metacentre that is assumed to be at a fixed point within small angles of heel.


