Stability -I : Chapter 1

Ullage = ( 10 – 9.708)
                 = 0.292m

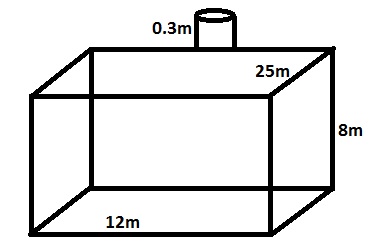
5. A rectangular tank measuring 25mx 12m x8m has an ullage pipe projecting 0.3m above the tank top. find the mass of SW in the tank when the ullage is 3.3m.

Solution :

Volume of the rectangular tank = ( L x B x H)
= (25 x 12 x 8 )

Pipe above the tank top is 0.3m

Total ullage =3.3m

Ullage inside the tank = (3.3 – 0.3)
= 3m

Depth of the SW = (8 – 3)
= 5m

Volume of the SW = (L x B x H )
= ( 25 x12 x5)
= 1500 m³

Mass of the SW = (volume x density)
                                 = (1500 x1.025)
                                 = 1537.5 t

6. A rectangular tank measures 30mx 16mx 14m. It has an ullage pipe projecting 0.5m above its top. Oil of RD 0.78 is to be loaded . The pipe line leading from the refinery to the ship is 10km long and 40cm in diameter. At the time of completion, all the oil in pipeline has to be taken. find at what ullage the valve at the refinery end must be shut so that the final ullage in the ship’s tank would be 0.78m. State also, the mass of oil loaded finally. (Assume π to be 3.1416).

Given :

The volume of the rectangular tank = (L x B x H)
=(30 x16 x14)
Ullage pipe projecting above its top = 0.5m
RD of oil = 0.78
The length of the pipe line from tank to the ship = 10km
= 10000m
The diameter of the pipe = (d)
= 40cm
Hence, radius = (40 /2 )
= 20cm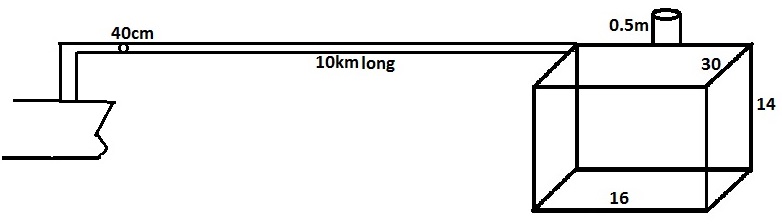

Volume of the tank = (L x B x H)
= (30m x16m x14m)
 =6720m³

Area = (L x B)
 = (30 x 16)
 = 480m²

The total ullage =0.78m

So ,ullage inside the tank = (0.78 –  0.50)
= 0.28m

If ullage inside the tank = 0.25m,The depth of oil to be loaded is
 = (14 -0.28) m
 =13.72m

Volume of the oil = (L x B x D)
=( 30x 16x 13.72)m
= 6585.6 m³

Mass of the oil to be load = (volume x density)
= (6585.6 x 0.78)
= 5136.768 t

Now , volume of oil in the pipe  = (πr²h)
 =(3.1416 x 0.2 x 0.2 x 10000)
=1256.64m³

Depth of oil when it poured in to the tank = (volume /area)
= (1256.64 /480)
= 2.618m

Depth of the tank without the pipe line oil = (13.72 -2.618)
 = 11.102m

Thus the ullage will be = (14 -11.102)
= 2.898m