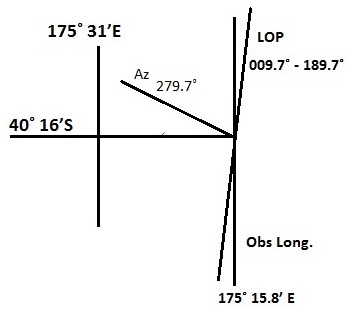
-
On 19th Jan 2008, PM at ship in DR 40˚ 16’S 175˚ 31’E, the sextant altitude of the sun’s LL was 43˚ 27.4’ when the GPS clock showed 03h 48m 00s. If IE was 1.5’ on the arc & HE was 22m, find the direction of the LOP and the longitude where it cuts the DR latitude.
d h m s
GMT 19 03 48 00
LIT (E) (+) 11 58 04
LMT 19 15 46 04
GMT 19 Jan 03h 48m 00s
GHA (19d 03h) 222˚ 23.0’ Dec S 20˚ 28.9’
Incr. (48m 00s) 012˚ 00.0’ d(-0.5) 00.4’
GHA 234˚ 23.0’ Dec S 20˚ 28.5’
Lat 40˚ 16’ S
Sext Alt 43˚ 27.4’
IE (on) (-) 01.5’
Observed Alt 43˚ 25.9’
Dip (HE 22m) (-) 08.3’
App Alt 43˚ 17.6’
T Corrn. LL (+) 15.2’
T Alt 43˚ 32.8’
NOTE:
In the following formula, if the LAT and DEC are of same name then sign is (-), If of contrary names then sign is (+).
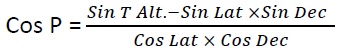
P = 49˚ 38.8’
Since, sight is after mer. Pass. ,so LHA = P
NOTE:
- Before meridian passage (Mer. Pass.) , LHA wil be between 180 and 360. After meridian passage, LHA will be between 000 and 180.So, to calculate LHA,
- If it given that the sight is taken AM at ship or meridian of east, then P = LHA.
- If it is given that the sight is taken at PM at ship, then P = 360 – LHA
- When P>90, the minus sign obtained for the value of A is to be ignored and is taken care by changing the name of A.
LHA = 049˚ 38.8’
GHA = 234˚ 23.0’
Long. W = 184˚ 44.2’
Obs. Long. = 175˚ 15.8’ E
We know that:
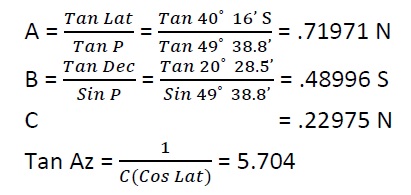
Azimuth = N 80.3˚ W
T Az= 279.7˚ (T)
LOP = 009.7˚ – 189.7˚
-
On 31st Aug 2008, PM at ship in DR 10˚15’S 000˚ 00’, the sextant altitude of the sun’s LL was 34˚ 54.0’ when the chron (error 01m 20s FAST) showed 03h 11m 30s. If IE was 1.5’ on the arc & HE was 17m, find the direction of the LOP and the longitude where it cuts the DR latitude.
GMT 31 August 15h 10m 10s
GHA (31d 15h) 044˚ 58.0’ Dec N 08˚ 21.4’
Incr. (10m 10s) 002˚ 32.5’ d(-0.9) 00.2’
GHA 046˚ 30.5’ Dec N 08˚ 21.2’
Lat 10˚ 15’ S
Sext Alt 34˚ 54.0’
IE (on) (-) 01.5’
Observed Alt 34˚ 52.5’
Dip (HE 22m) (-) 07.3’
App Alt 34˚ 45.2’
T Corrn. LL (+) 14.6’
T Alt 34˚ 59.8’
NOTE:
In the following formula,
- if the LAT and DEC are of same name then sign is (-),
- If of contrary names then sign is (+) .
P = 46˚25.5’
Since, sight is after mer. Pass. ,so LHA = P
LHA = 046˚ 25.5’
GHA = 046˚ 30.5’
Long. W = 000˚ 05.0’
Obs. Long. = 000˚ 05.0’ W
We know that :
Azimuth = N 69.8˚ W
T Az= 301.8˚ (T)
LOP = 031.8˚ – 211.8˚
-
On 22nd Sept 2008, PM at ship in DR 48˚ 20’N 085˚ 40’E, the sextant altitude of the sun’s UL was 20˚ 04.9’ when the GPS clock showed 10h 09m 38s. If IE was 2.2’ on the arc & HE was 25m, find the direction of the LOP and the longitude where it cuts the DR latitude.
d h m s
GMT 22 10 09 38
LIT (E) (+) 05 42 40
LMT 22 15 52 18
GMT 22 Sept 10h 09m 38s
GHA (22d 10h) 331˚ 51.4’ Dec N 00˚ 05.6’
Incr. (09m 38s) 002˚ 24.5’ d(-1.0) 00.2’
GHA 334˚ 15.9’ Dec N 00˚ 05.4’
Lat 48˚ 20’ N
Sext Alt 20˚ 04.9’
IE (on) (-) 02.2’
Observed Alt 20˚ 02.7’
Dip (HE 25m) (-) 08.8’
App Alt 19˚ 53.9’
T Corrn. UL (-) 18.4’
T Alt 19˚ 35.5’
NOTE:
In the following formula,
- If the LAT and DEC are of same name then sign is (-),
- If of contrary names then sign is (+) .
P = 59˚ 48.8’
Since, sight is after mer. Pass. ,so LHA = P
LHA = 059˚ 48.8’
GHA = 334˚ 15.9’
Long. E = 085˚ 32.9’
Obs. Long. = 085˚ 32.9’ E
We know that :
Azimuth = S 66.7˚ W
T Az = 246.7˚ (T)
LOP = 156.7˚ – 336.7˚
-
On 5th March 2008, AM at ship in DR 38˚ 11’S 151˚ 10’E, the sextant altitude of the sun’s LL was 35˚ 59.1’ when the chron (error 00m 46s SLOW) showed 10h 54m 54s. If IE was 1.3’ off the arc & HE was 30m, find the direction of the LOP and the longitude where it cuts the DR latitude.
GMT 04 March 22h 55m 40s
GHA (04d 22h) 147˚ 06.9’ Dec S 06˚ 01.3’
Incr. (55m 40s) 013˚ 55.0’ d(-1.0) 00.9’
GHA 161˚ 01.9’ Dec S 06˚ 00.4’
Lat 38˚ 11’ S
Sext Alt 35˚ 59.1’
IE (off) (+) 01.3’
Observed Alt 36˚ 00.4’
Dip (HE 30m) (-) 09.6’
App Alt 35˚ 50.8’
T Corrn. LL (+) 14.9’
T Alt 36˚ 05.7’
NOTE:
In the following formula,
- If the LAT and DEC are of same name then sign is (-),
- If of contrary names then sign is (+) .
P = 47˚ 52.9’
Since, sight is before mer. Pass. ,so LHA = 360 – P
LHA = 312˚ 08.1’
GHA = 161˚ 01.9’
Long. E = 151˚ 06.2’
Obs. Long. = 151˚ 06.2’ E
Azimuth = N 65.9˚ E
T Az = 065.9˚ (T)
LOP = 155.9˚ – 335.9˚
-
On 30th April 2008, in DR 00˚ 20’N 060˚ 12’W, the sextant altitude of the sun’s UL East of the Meridian was 44˚ 13.4’ when the GPS clock showed 01h 00m 52s. If IE was 3.1’ off the arc & HE was 20m, find the direction of the LOP and the longitude where it cuts the DR latitude.
d h m s
GMT 30 13 00 52
LIT (W) (-) 04 00 48
LMT 30 09 00 04
GMT 30 April 13h 00m 52s
GHA (30d 13h) 015˚ 42.7’ Dec N 14˚ 59.3’
Incr. (00m 52s) 000˚ 13.0’ d(+0.7) 00.0’
GHA 015˚ 55.7’ Dec N 14˚ 59.3’
Lat 00˚ 20’ N
Sext Alt 44˚ 13.4’
IE (off) (+) 03.1’
Observed Alt 44˚ 16.5’
Dip (HE 20m) (-) 07.9’
App Alt 44˚ 08.6’
T Corrn. UL (-) 16.8’
T Alt 43˚ 51.8’
NOTE:
In the following formula,
- If the LAT and DEC are of same name then sign is (-),
- If of contrary names then sign is (+)
P = 44˚ 17.5’
Since, sight is before mer. Pass. ,so LHA = 360 – P
LHA = 315˚ 42.5’
GHA = 015˚ 55.7’
Long. W = 060˚ 13.2’
Obs. Long. = 060˚ 13.2’ W
We know that :
Azimuth = N 69.31˚ E
T Az = 069.31˚ (T)
LOP = 159.3˚ – 339.3˚
@vikarant_sharma diagram in first question is wrong obs long value is smaller than DR LONG so it should be drawn in left side of DR long
can you tell how you have calculated gmt in 1st question
2nd and 3rd point of the note is also wrong. Correct one is when the sun (and star) is east of the meridian it’s AM, at that time LHA is between 180-360 so P= 360°-LHA. when the sun and (the star) is west of the meridian at that time LHA is between 0°-180° , and LHA=P . Correct ans of the question is P= 49°38.8°… long=175°15.8°…. az=N80.1W or 279.9° true
The value of P is wrong. It should be 52°0.1′. Hence LHA would be 52°0.1′ and longitude = 004°29.6’E
Calculate latitude course and speed error for following ship
A)ship steering 230°T at 22.0 knots in latitude 41°24S
B)ship steering 140°T at 15.0 knots in latitude 56°00N
Please solve this problem argent machinical project hy
Its wrong
Can u tell how did you got the GMT time to be 13h 00m 52s in the last question?
No
No its wrong
thank you very much Lovepreet for notifying us.. we will look into it & correct as required.best wishes for your exams.
solutions of formula cosP is wrongg … it matches the ans in the textbook bt when we try to solve it ans is slight different.. so it is humble request to u to pls correct the answers because students are facing difficulties when trying to get help from youe site …
Thank.you lovepreet..can you please specify the numerical where it is wrong.