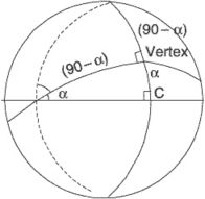
The vertex of a great circle is the maximum latitude point of the great circle.
The vertex has the following properties:
There is a maximum latitude point in both the northern and southern hemispheres; these points have the same value of latitude (eg if northern vertex = 40°N then southern vertex = 40°S). The longitudes of the vertices are 180° apart (e.g. if one is in 20°W, the other is in 160°E).
At the vertex the course on the great circle is exactly 090°T or 270°T, depending on whether you are proceeding towards the east or the west. This means that the angle between the great circle and the meridian at the vertex is always 90°.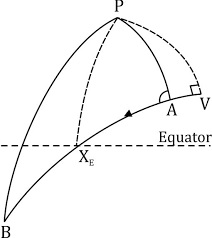

Leave a Comment