In Other words, we can understand the great circle as:
A great circle is the shortest path between two points along the surface of a sphere. A great circle is the intersection of the surface with a plane passing through the center of the planet.
The equator and all meridians are great circles. All great circles other than these do not have a constant azimuth, the spherical analog of slope; they cross successive meridians at different angles. The Gnomonic Projection represents arbitrary great circles as straight lines.
Great circles are examples of geodesics. A geodesic is the shortest possible path constrained to lie on a curved surface, independent of the choice of a coordinate system.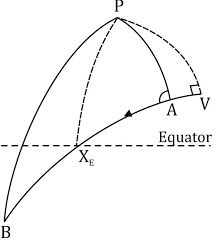



Great post! I’ve always been curious about Great Circle Sailing and its significance in navigation. The way you explained the concept and its advantages really helped clarify my understanding. Looking forward to more insightful articles!