Stability -I : Chapter 1

Hence, Ullage = (12-11.76)
                           = 0.24m.

4. A tank 10m deep has vertical sides .its bottom consist of triangle 12mx12mx10m. find the mass of oil (of RD0.800) to be loaded , allowing 3 % of the volume of oil loaded for expansion. State the ullage on completion of loading.

Solution:

Depth of the tank = 10m
L, B, H, of triangle = (12 x 12 x 12
RD = 0.8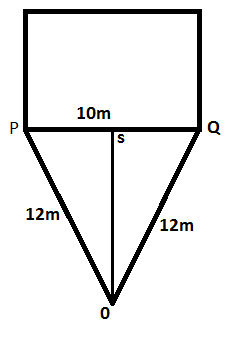

Allowing, 3% of the volume of the oil loaded for expansion.
Area of the triangle = 1/2 (base x height)

In triangle PQR, RQ in the height which divide the base at same length.
So In triangle PSR

SR² =PR² –PS²
= (12²– 5²)
= (144 -25)
=119

So, SR = 10.9m
So area of the triangle = 1/2 (10×10.9)
=54.5m²

Volume of the tank = (10 x54.5)
= 545m³

Now, volume of the oil = (Total volume -free space)

let ‘V’ be the volume of the oil
545 = (V + 3/100 x V)
545 = (V + 3V/ 100)
545 = (103V /100)
V = (545 x 100) /103
V = 529.126m³

Mass of the oil = (density x volume)
= 0.8 x 529.126
=423.3 t

Depth of the oil = (volume of oil)/(area)
= (529.126 /54.5)
= 9.7087m