Initial Transverse Metacentre Is defined as the point of intersection of successive lines of action of buoyancy force (Bf) when the ship is in the initial upright condition and subsequently heeled conditions.
It is assumed to be at a fixed position when the ship is heeled within small angles only.
Consider the ship shown.
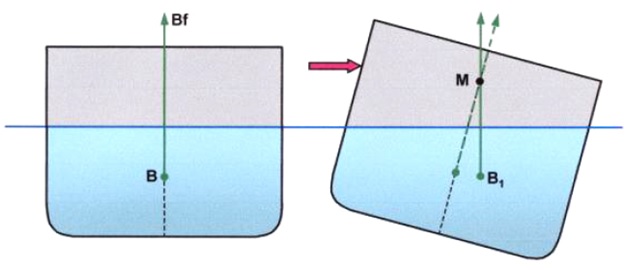
When the ship heels beyond small angles the point of intersection has to move, hence the term Initial Transverse Metacentre.
It’s position is expressed as a height above the keel in metres and is termed KM. The value of KM is tabulated in ship’s hydrostatic data and its position varies with draught.

Leave a Comment