If a stone was being swung in a circular path by a string and if the length of the string was suddenly decreased (radius of rotation of the stone suddenly decreased), it will be observed that the speed of rotation of the stone increases.
Similarly, as the radius of rotation of the wind in a TRS decreases, due to its spirally inward movement, the wind speed increases.
As the wind speed increases, a new force called “Centrifugal force” or “Cyclostrophic force” comes into being. This force acts radially outward from the centre of rotation (low pressure area). The greater the speed of the rotation, the greater the Cyclostrophic force. Cyclostrophic force therefore, increases steadily from practically nil at the outer fringes of the TRS to maximum in the eye-wall.
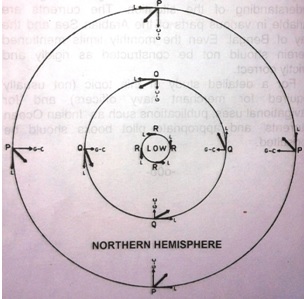
In the figure, P is a point on the outer fringes of a TRS, R a point in the eye-wall and Q, a point about midway between P & R.
At P, gradient force (G) acts radially inwards while Cyclostrophic force (C) acts radially outwards. The latter is negligible at the outer fringes of the TRS. The resultant of G and C is as shown in the figure. The wind that finally blows at P is the resultant of G-C and the Coriolis force (L), and has angle of indraft of about 45˚.
At Q, Cyclostrophic force has reached a certain amount and G-C is now less than before, as shown in the figure. The wind that blows at Q is the resultant of G-C and L and has an angle of indraft of about 22˚.
At R, Cyclostrophic force has increased to such an extent that it is now equal to gradient force (G-C=Zero), there is no inward force at all. The wind that blows as a resultant of G-C and L, hence blows in a perfectly circular path (i.e. with an angle of indraft of 0˚).
This is why or how:
