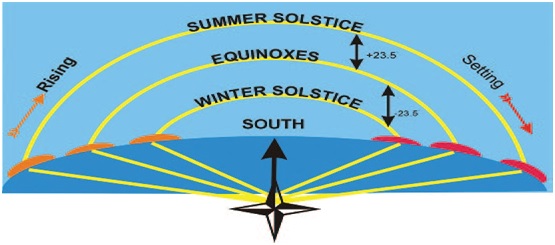
A celestial body’s amplitude angle is the complement of its azimuth angle. when the body rises or sets, the amplitude angle is the arc of the horizon between the body and the East/West point of the horizon where the observer’s prime vertical intersects the horizon (at 90°). In practical navigation, a bearing of a body can be observed when it is on either the celestial or the visible horizon. To determine compass error, simply convert the computed amplitude angle to true degrees and compare it with the observed compass bearing.
To calculate a body’s amplitude we need to know
- declination of the body
- latitude of the observer
Lacking tables you need a calculator that can handle simple trigonometry
The general formula is:
Amplitude=sin−1(sin declination of body/cosine observer’s latitude)
It does not contain an altitude term because the body’s computed altitude is zero at this instant. The angle is prefixed E if the body is rising and W if it is setting. This is the only angle in celestial navigation referenced from East or West, i.e. from the prime vertical. A body with northerly declination will rise and set North of the prime vertical. Likewise, a body with southerly declination will rise and set South of the prime vertical. Therefore, the angle is suffixed N or S to agree with the name of the body’s declination. A body whose declination is zero rises and sets exactly on the prime vertical. The Sun is on the celestial horizon when its lower limb is approximately two thirds of a diameter above the visible horizon. The Moon is on the celestial horizon when its upper limb is on the visible horizon.
When observing a body on the visible horizon, a correction must be applied. This correction accounts for the slight change in bearing as the body moves between the visible and celestial horizons. It reduces the bearing on the visible horizon to the celestial horizon, from which the table is computed.
For the Sun, stars, and planets, apply this correction to the observed bearing in the direction away from the elevated pole. For the moon, apply one half of the correction toward the elevated pole. Note that the algebraic sign of the correction does not depend upon the body’s declination, but only on the observer’s latitude.
Even if the declination and your latitude have different names, i.e, one is north and the other is south, all the figure are taken as positive. Once you have the answer you will need to convert it into a bearing as shown in Figure
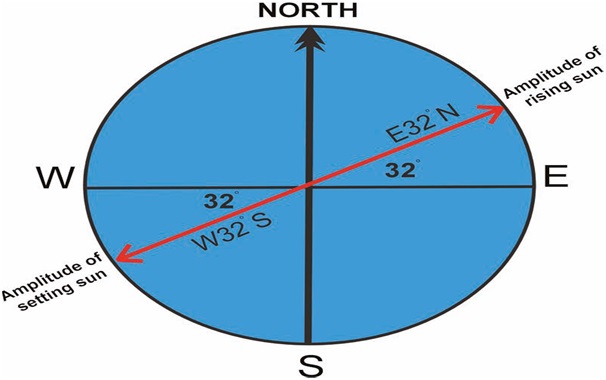
An amplitude is taken when a celestial body is exactly on the horizon. Imagine you are watching the sun rise at 41⁰N and the sun’s declination is 23.5⁰N.
Amplitude = sin−1 (sin 23.5 divided by cos 41)
= sin−1 (0.3987 divided by 0.7547)
= sin−1 (0.5283)
= 31.8899 Degree ,= 32⁰