Stability – I : Chapter 8

10. A barge of 45m long has a uniform transverse cross-section throughout, which consists of a rectangle above a triangle. The rectangle is 8m broad and 4m high. The triangle is apex downwards 8m broad and 3m deep.if she displacement of the barge is 1620t, find the position of its COB with reference to the keel and also with reference to the after and , if it is upright and on an even keel in FW.

Solution:

Total displacement = 1620t

Let ‘X’  t  of weight which is  not displaced by triangle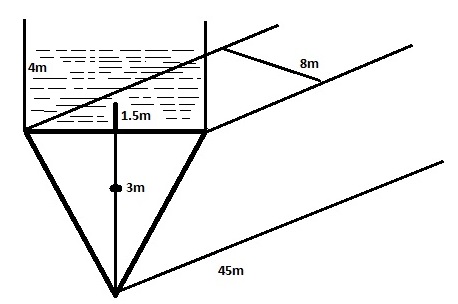

So weight displaced  is (1620 – X )t

Area of triangle = ½ ( L x B x H)
= (1/2 x 45 x 8 x 3)
= 540m3

Displacement (W) = (u/w volume) x (density)
= 540 x 1
= 540t  = X( as per assumption made above  in solution )

Displacement of rectangle = (1620 – X)
= (1620 – 540)
= 1080t

Now ,displacement for rectangle = (u/w volume) x (density)
1080 = (45 x 8 x draft)  x (1)
Hence, draft = 1080/(45 x 8)
draft = 3 m

for calculating COB = (draft/2)
= (3/2)
= 1.5m

So, COB with respect to keel = (3.0 + 1.5)m
= 4.5m .

Now, VM ( vertical moment) created by triangle:
=(W x d)
= (540 x 2)
= 1080 tm.

Now , VM ( vertical moment) created by rectangle:
= (W x d)
= (1080 x 4.5)
= 4860 tm.

final vertical moment = ( VM) _triangle  + (VM) _rectangle
Final Weight = 1620t

We know that:
Final KB = (Final VM / Final W)
= (5940/ 1620)
= 3.66 m