Stability – I : Chapter 8

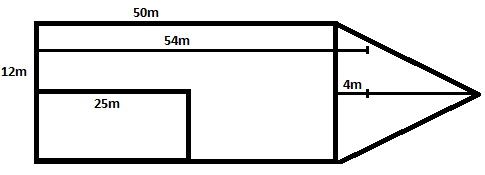
9. The deck and keel of a flat-bottomed barge and identical. Its sides are vertical. The deck consists of two section – the bow is a triangle 12m broad and measures 12m in the fore and aft direction ; the mid-body is a rectangle 50m long and 12m broad . if it is floating on an even keel in SW with a displacement of 3444t , find the position of its COB with reference to its after end .

Solution;

Total displacement = 3444t

Displacement (W) = (u/w volume ) x (density)
3444     =    (u/w volume of triangle ) + (u/w volume of rectangle )     x (1.025)
3444    =    (( 1/2 x 12 x 12 x d)  + ( 50 x 12 x d) )  x 1.025
3444   =    (72 d + 600 d) x 1.025
3444 =    (672d x 1.025)
3444 = 688.8 d

So, d = 3444/ 688.8
d =  5 m

now, COB =(draft/2)
=(5/2) m
=  2.5 m with reference to keel

Now for calculating COB with reference to after end
Total moment of barge = (moment of triangle)  + (moment of rectangle)
(3444 x LCB of barge) = ( u/w volume )x (density) x(LCB)  + (u/w volume ) x (density ) x (LCB)
(3444 x LCB)  = (1/2 x 12 x 12  x 5)  x (1.025) x( 54)  +   (50 x 12 x 5 ) x (1.005 ) x (25)
(3444 x LCB) = (19926)  + (76875)
(3444 x LCB)      = 96801
LCB = (96801 / 3444)
= 28.10m.