Stability – I : Chapter 8

7. A cylindrical drum of 0.8m diameter and 1.5m height weight 10kg. 490 kg of steel is put in it such that it floats with its axis vertical in FW. find its KB . (Assume π to be 22/7 ).

Solution :

Diameter = 0.8m ,
So, radius = (0.8 /2) = 0.4m

Height = 1.5m
Weight = 10kg = (0.01) t
Mass of steel = 490kg = 0.49t
Total displacement = (0.01 + 0.49)
= 0.50t

Displacement (W) = (u/w volume) x (density)
0.5 =  r² d) x  (RD)
0.5 = (3.1416 x 0.4 x 0.4 x d) x (1)
So, d = 0.5/(3.1416 x 0.4 x 0.4) x(1)
= 0.995m

Again, KB can be calculated as = (draft/2)
= 0.4975m

8. A barge prism shaped such that its deck and keel are identical and parallel ; its side vertical .its deck consists of three shapes triangular bow of 12m each side ; rectangular mid-part 80m long and 12m wide ; semi-circular stern of radius 6m . If the light displacement of the barge is 500t and it has 5000t of cargo in it, find its KB when floating on an even keel in SW. (Assume π to be 3.142 )

Solution:

According to the question the drawn figure can consist of 3 difference structure ; namely  triangle BEC , rectangle ABCD, semicircle  AFD .

Total displacement = (5000 + 500)
= 5500t

As we know that:
Total displacement = (Total u/w volume) x (density)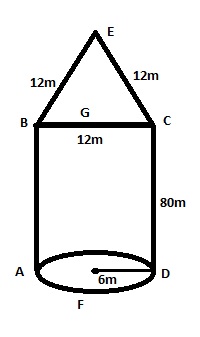

Total u/w volume = (volume of  triangle BEC) + (Volume of rectangle ABCD) + (Volume of semicircle AFD)

Area of triangle BCE   = (π r²   /2)
= (3.14 x 6 x 6 )/ 2
= 56. 556m²

Area of rectangle ABCD = (L X B )
= (80 x 12)
= 960m²

Area of semicircle   AFD   = (1/2 x b x h)
= (1/2 x 12 x 10.39)
= 62.34m²

In triangle BEC,  EG is the height

So , EG² = BE² – BG²
EG² = 12² -6²

 ⁼    144 – 36
=108
EG = 10.39m

Hence, Total area = (56.55 + 62.34 + 960.0)
= 1078.89m²

Displacement (W)= (u/w volume) x (density)
5500 = (Area x depth) x (density)
5500 = (1078.89 x d ) x (1.025)

Draft = 5500 /(1078.89 x 1.025)
= 4.97m

Now, KB = (draft)/2
= (4.97/2)
= 2.485m.