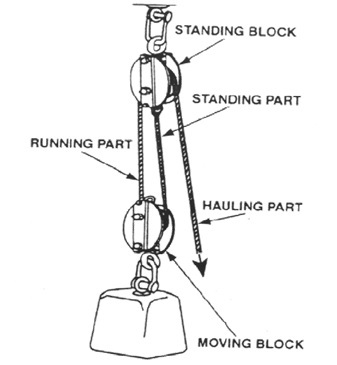
The mechanical advantage, if one ignores the effect of friction, is simply equal to the number of falls pulling on the load. And Falls are the Parts of the line stretching between the blocks as shown in the diagram. So, a tackle which has four falls will have a mechanical advantage of 4.This means that a 100 kgs weight can be lifted by exerting only 25 kgs of force on the hauling part. The mechanical advantage or purchase of a tackle will, in theory increase by the number of sheaves in the blocks. To calculate the mechanical advantage of a purchase you count the no. of sheaves within the purchase.
For example, a purchase with a double block and a single block would have three sheaves and therefore have a mechanical advantage of 3.
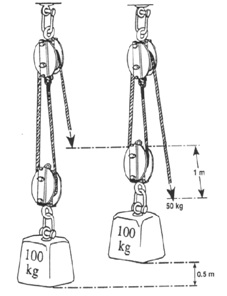
Mathematically, Mechanical advantage is the ratio of the load to effort.
M.A. = LOAD / EFFORT
& velocity ratio is the ratio of velocity of effort is to velocity of load or distance effort moves is to distance load moves.
V.R. = DISTANCE EFFORT MOVES/DISTANCE LOAD MOVES
WORK PUT IN BY EFFORT = WORK DONE ON LOAD + WORK SPENT IN OVERCOMING FRICTION
EFFORT X DE = (LOAD + n X 10% X LOAD) X DL (where, n is the no. of sheaves & D is distance)
EFFORT = (LOAD + n X 10% X LOAD) X (DL) ( DE)

Let’s go through an example. We want to lift a five tonne weight and we want to use a three fold purchase (six sheaves). The purchase is to be rigged to disadvantage. Using the formula above:
Weight = five tonne
N = 6
V.R. = 6 (rigged to disadvantage)

Stress = 1.33 tonnes
Therefore, we need a line with a SWL that exceeds this figure.

