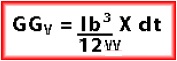What is Free Surface Effect (FSE)?

Consider the ship shown with a partially filled tank. Imagine the liquid in the tank is frozen and the ship is heeled to a small angle.

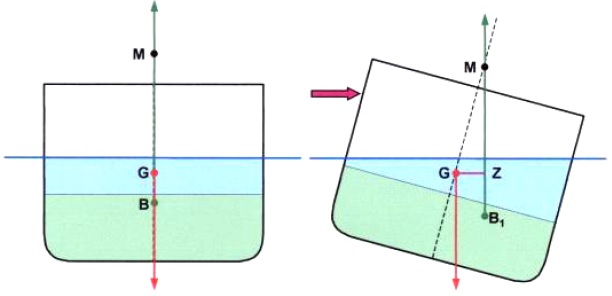
In the heeled condition GZ is the righting lever. Because the liquid is frozen it acts as a static weight and does not move.

Consider what will happen if the liquid in the tank thaws out and is then free to move as the ship heels, as would normally be the case.

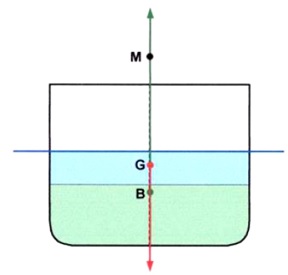
In the initial upright condition everything appears as normal.

But note what happens as the ship is again heeled by an external force to the same small angle of inclination.

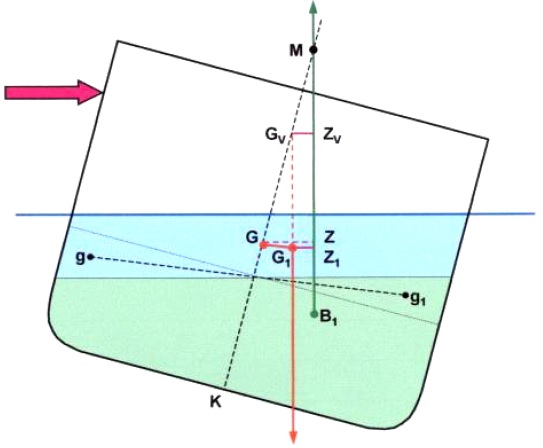
A wedge of the liquid is transferred to the low side of the ship (gg₁).
Since weight has shifted G moves parallel and in the same direction as the shift of the weight (GG₁).

This causes the righting lever to be reduced from GZ to G1Z1.

 The righting lever G₁Z₁, is the same as the GZ that would have existed had G been raised to G_V.
GG_V represents the virtual rise of G that results from the free surface effect of the slack tank.
(G does not actually rise, but the movement of the liquid in the tank has the same effect on GZ values as if G had actually been caused to rise – hence the term ‘virtual rise of G’!)

Thus:
GM is termed the solid GM ;
G_V M is termed the effective or fluid GM.

When calculating the GM of a ship it is important that the effects of free surfaces in slack tanks are considered. The loss of GZ will be greater as the number of slack tanks increases, i.e. the cumulative effect of all slack tanks must be accounted for.

It is always the fluid GM that must be determined to take account of the reduction in GZ values that arises from liquid movement within the ship as it is heeled.

When the ship returns to the upright condition the centre of gravity (G1) will move back to its original position at G as the liquid in the tank finds its own level.

Remember; G does not actually move up to G_V.

For a tank that has a rectangular free surface the virtual rise of G in metres can be calculated by:

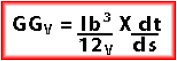
where:                    

 GG_V  is the virtual rise of G in metres;
L is the tank length;
b  is the tank breadth;
dt is the density of the liquid in the tank;
ds  is the density of the water in which the ship floats (1.025 t/m3);
  V  is the volume of displacement of the ship.

Since:

DISPLACEMENT = VOLUME OF DISPLACEMENT × DENSITY

i.e.                                           W = V x ds

it follows that: