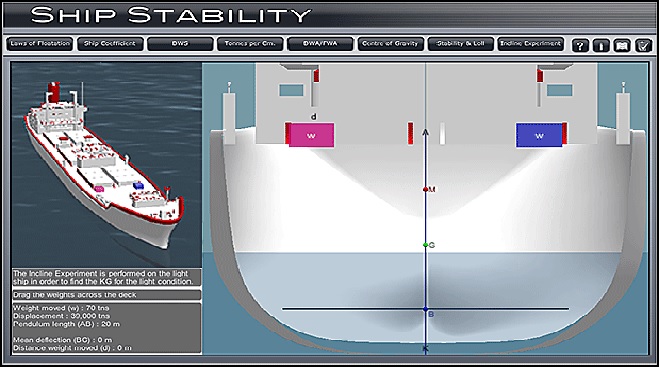
A ship is in an unstable condition if, when heeled by an external force in still water to a small angle, it continues to heel further when the external force is removed.
Consider a ship that is floating upright in still water with G and B as shown. The initial transverse metacentre (M) is below G.
i.e. KM – KG = GM; which has a negative value
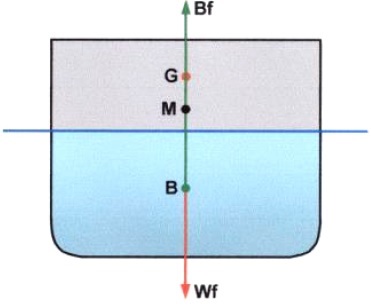
The ship now heels to a small angle of inclination.
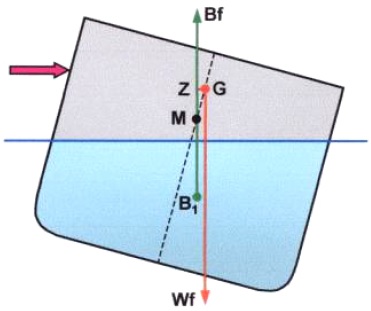
Consider the lines of action of Wf and Bf. They are acting in such a way to cause the ship to heel further over. GZ is a capsizing lever!
The question that now comes to mind is: Will the ship capsize?
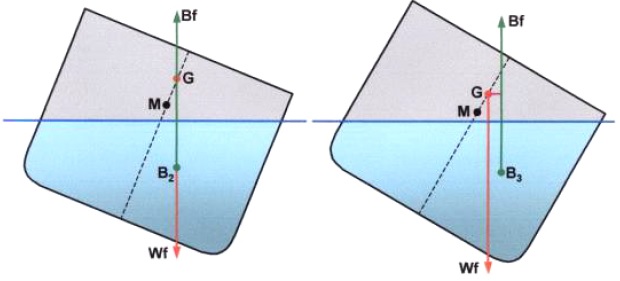
Possibly! As the ship continues to heel, the centre of buoyancy (B) will move outward as the underwater volume of the ship changes shape.
Provided that the centre of buoyancy can move sufficiently outboard to attain a new position vertically below G then the capsizing lever will disappear and the ship will come to rest at an angle of loll. If the centre of gravity were very high then the ship would possibly capsize.
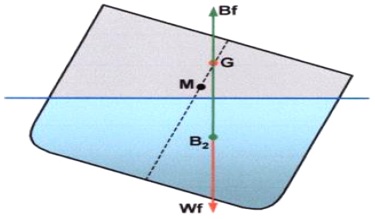
If the ship is heeled beyond the angle of loll the centre of buoyancy (B) will move outboard of the centre of gravity (G). This causes a positive righting lever (GZ) that will act to return the ship back to the angle of loll.
